(선형대수와 통계학으로 배우는 머신러닝 with 파이썬) 4. 머신러닝을 위한 통계학(2)

모집단, Population과 표본, Sample

모집단이란 조사하려고 하는 대상 전체, 집단을 뜻한다.

모집단의 특성을 나타내는 대표값을 모수, Population parameter이라고 한다.

표본이란 모집단에서 특정 일부를 추출한 것이다.

표본의 대표값을 표본 통계량, Sample statistic이라고 한다.

인공지능에서 모수와 표본 통계량은 각각 Parameter, Sample이라고 한다.

평균, Mean or Expectation

평균에는 산술 평균, 기하 평균, 조화 평균 등 여러 종류에 평균이 있다.

\[E(X) = \mu\]

모평균

모평균, Population Mean이란 모집단의 평균을 의미한다.

조사하려는 대상 전체의 평균을 뜻한다.

산술 평균, Arithmetic Mean

단순히 모든 데이터값, 모집단을 덧셈한 후 데이터 개수로 나누는 것을 의미한다.

확률에 대한 기댓값

\[\bar{X} = \frac{1}{n}\sum_{i=1}^{n}x_{i}\]

모평균의 추정량, 표본 평균(Sample Mean)

$$ E(X) = \sum_{x}xp(x),

이산형

\[E(X) = \sig_{\infty}^{\infty}xf(x)dx\]

연속형

평균의 의미

평균은 모집단에서 가장 크게 분포 돼 있는 부분이다.

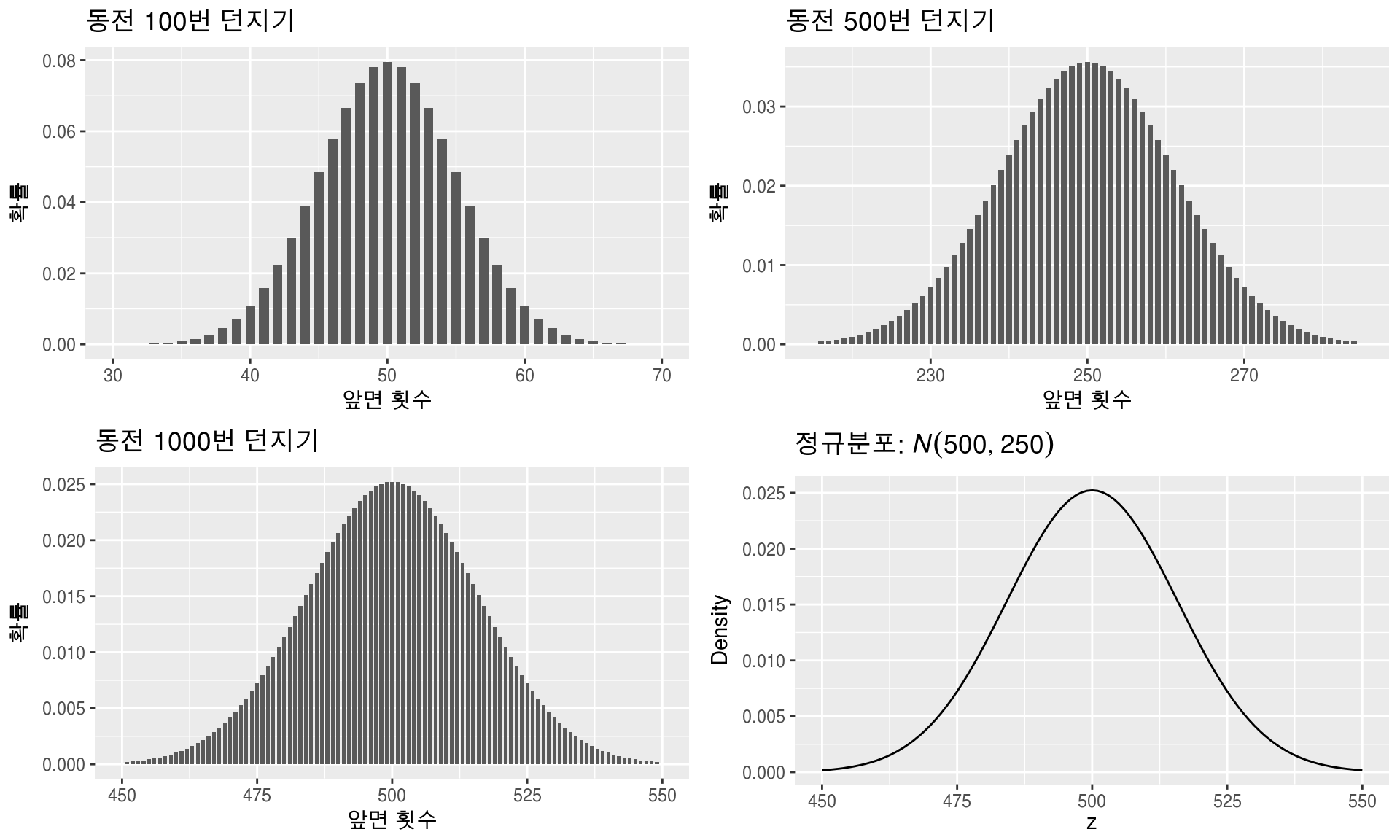평균 그래프^[1]

분산, Variance

모집단의 분포가 얼마나 퍼져 있는지를 수치화한 것이다.

\[Var(X)\]

분산은 평균에 대한 편차 제곱의 평균으로 계산한다.

편차, deviation란? 관측값과 평균의 차이를 말한다.

$d = X - \mu$ or $d = y - \hat{y}$

따라서 위의 말을 식으로 풀어보면 다음과 같다.

모 분산, Population variance

모집단^$A$의 분산^Variance으로서 다음과 같이 표현한다.

\[Var(X) = E[(X-\mu)^{2}] = \sigma^{2}\]

편차 제곱을 평균한 것이다.

$\sigma$는 표준 편차를 뜻한다.

분산을 표현했던 $E[(X-\mu)^{2}]$ 를 분리하여 표현할 수 있다.

\[Var(X) = E[(X-\mu)^{2}]\] \[\;\;\;\;\;\;\;\; = E[X^{2} - 2\mu X + \mu^{2}]\] \[\;\;\;\;\;\;\;\; = E(X^{2}) - 2\mu E(X) + \mu^{2}\] \[\;\;\;\;\;\;\;\; = E(X^{2}) - \mu^{2}\]

모집단을 평균으로 뺀 값에 제곱값의 평균은 모집단의 제곱값의 평균을 평균제곱값으로 뺀 값과 같다.

표본 분산, sample variance

표본 분산, 샘플 값이 가지는 분산은 다음과 같이 표현한다.

\[\hat{\sigma}^{2} = s^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}\]

모집단의 샘플에 대한 분산은 $ \hat{\sigma} $ 로 표현하고 Sample variance의 s로 표현한다.

자유도, degree of freedom

변수의 자유로움에 대해 나타내는 것이다.

표본 분산의 식을 보면, 표본 평균인 $\bar{x}$가 포함돼있는 것을 알 수 있다.

이가 뜻하는 바는, 분산을 구하는 시점에 이미 표본 평균은 정해져있다는 것이다.

따라서 분산을 구하는 시점에서 데이터가 n개 있다고 가정했을 때 자유롭게 정할 수 있는 데이터는 n-1개 뿐이다.

표본 평균이 정해졌기 때문에 정할 수 있는 값은 n-1개라는데 나중에 분명히 까먹을거같다.

표준 편차, standard deviation

분산과 비슷한 개념으로 분산의 양의 제곱근으로 정의된다.

분산을 구하는 과정에서 편차를 제곱하는 과정에서 분산 값 자체의 의미 파악이 어렵다.

제곱근을 통해 원래 단위로 돌아가는 과정을 얻을 수 있다.

\[\sigma = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}\]

머신러닝에서 평균과 분산을 알면 분포를 그려보지 않아도 추측하기 쉬워진다.

데이터의 흩어진 정도를 알 수 있다.

평균과 기댓값에대해^[2]

통계를 공부하다보니 평균과 기댓값에 대한 용어에 혼란이 와서 위 블로그를 참고해봤습니다.

평균과 분산

평균과 분산은

참고문헌

1. Chapter 3 정규분포(Normal distribution), 기초통계 개념정리, 김진섭, https://bookdown.org/mathemedicine/Stat_book/normal-distribution.html

2. 평균과 기댓값, heejin_park, 2020.06.15 작성, 2022.04.13 방문, https://infograph.tistory.com/191

← 이전 글로 다음 글로 →