Cross Entropy is?

엔트로피[Entropy]는 하나의 분포를 대상으로 하는 반면, 크로스-엔트로피는 두 분포 $P(x), Q(x)$를 대상으로 엔트로피를 측정해 두 분포 간의 차이를 계산합니다. 머신러닝GAN에서 크로스-엔트로피를 사용할 때는$P(x)$를 실제 모형의 분포, $Q(x)$를 추정 모형의 분포라고 설정합니다.[1]

교차 엔트로피cross entropy는 실제 결과가 도출될 우도와 우리가 생각하는 우도의 사이의 차이에 따른 결과의 불확실성에 대한 지표입니다. … 교차 엔트로피를 두 확률분포의 차이라고 생각할 수 있습니다. 두 분포의 차이가 없는 만큼 교차 엔트로피도 낮아집니다. 정확히 일치한다면 교차 엔트로피는 0입니다.[2]


Expressiion of Cross-Entropy

\[CrossEntropy(P, Q) = \sum -P(x)logQ(x)\]
$P$는 실제 확률의 분포, $Q$는 추정 모형의 분포이다.


Example

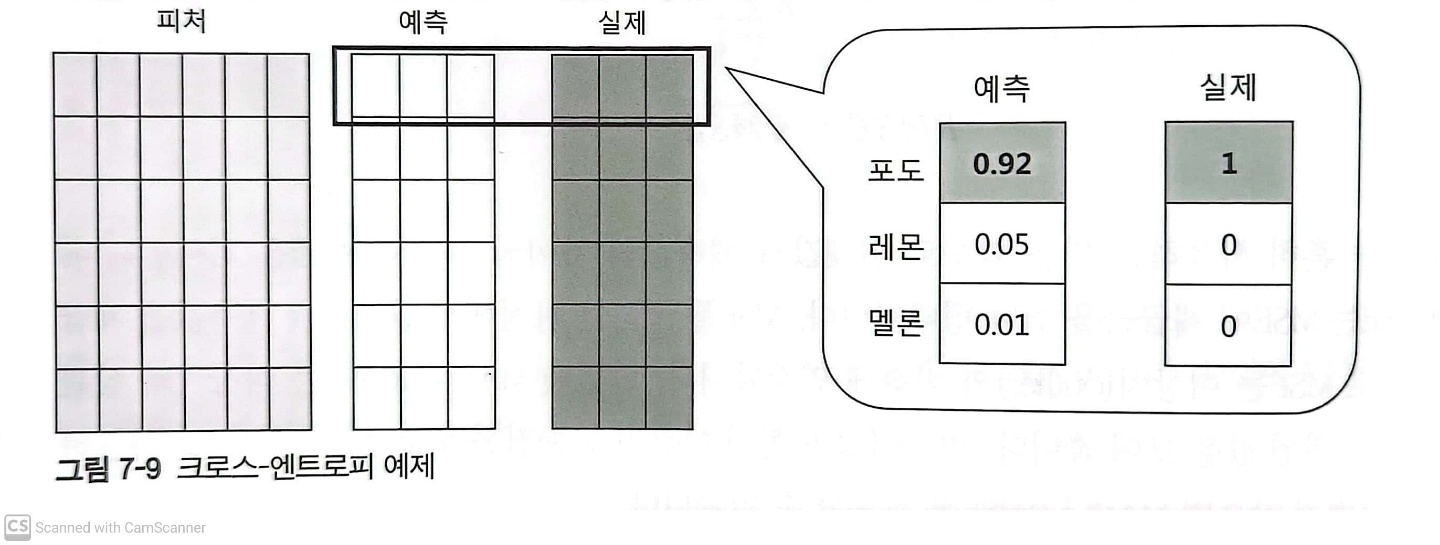
Cross-Entropy-Example

\[CrossEntropy(P, Q) = \sum -P(x)logQ(x)\] \[\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -(1 \times log0.92 \; + \; 0 \times log 0.05 \; + \; 0 \times log 0.01)\] \[\;\;\;\;\;\;\;\;\;\;= 0.08\]

Selection criteria for probabilities P and Q

Cross Entropy에서 두 확률 분포인 P와 Q를 위와같은 위치에 선정한 이유가 있다.

그 이유는 많은 데이터셋에서 정답 벡터는 다양한 확률값을 갖는 확률 분포가 아니라 선택될 원소 하나만 1이고 나머지가 모두 0인 원-핫 벡터 형태로 표현된다. 그런데 원솟값 모두가 0 혹은 1인 원-핫 벡터 성분들이 log 연산에 이용되면 1은 변별력 없는 0 값만 생성하고 0은 $-\infty$ 값을 결과로 하는 오류를 일으키게 된다.이 때문에 정답 벡터를 로그 연산의 대상이 되지 않는 확률 분포 P로 삼는 편이 유리하다.

Softmax를 적용한 결과를 Q로 지정할 때 문제점을 참고해봐도 좋다.

Reference

1. 7.5.4 엔트로피 156p, 선형대수와 통계학으로 배우는 머신러닝 with 파이썬, 장철원, 비제이퍼블릭

2. 부록. BCE 손실 246p, GAN 첫걸음, 타리크라시드 지음, 고락윤 옮김, 한빛미디어(주)