(파이토치 첫걸음) 3. 선형회귀분석

3장 서론

선형회귀분석이 데이터 분석과 딥러닝에서 가지는 의미와 손실 함수 와 경사하강법을 간단하게 배우고 실습할 수 있다.

선형회귀분석

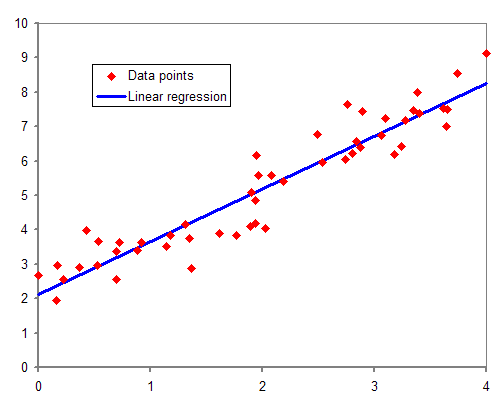
선형회귀분석_wikipedia

선형회귀분석은 간단히 설명하면 주어진 데이터를 가장 잘 설명하는 직선 하나를 찾는 것이다.

데이터 분포들(Data points)에 적합한 선형을 찾는 과정

선형은 $ y = wx + b $ 로 표현할 수 있다.

1차 방정식에서는 w는 기울기, b는 y 절편이다.

선형회귀분석에서는 w(Weight, 가중치), b(bias, 편차)로 표현한다.

손실 함수

학습 과정을 통해 선형회귀에 필요한 적절한 선형을 찾는다.

학습은 더 나은것을 찾아가는 과정으로 서, 값의 비교가 필요하다.

여기서 비교값은 $w$ 와 $b$로 가능하다

주어진 데이터값 $y$는 $wx + b$를 통해 알 수 있고

예측값 $\hat{y}$또한 예측한 $y, b$를 통해 알 수 있다.

하지만 무작정 예측(random value)를 통해 유추하기는 모든 경우의 수의 반복이 필요하여 비효율적이게 된다.

여기서 우리는 평균제곱오차, MSE^{mean squared error}를 사용한다.

$MSE = \frac{1}{n}\sum_{i=1}^{n}(\hat{y}-y)^{2}$

평균제곱오차를 사용하여 예측값과 주어진 데이터값의 최소값을 얻기 위해서는 손실함수, loss function 또는 비용함수, cost function를 사용한다.

$Error = \frac{1}{n}\sum_{i=1}^{n}(wx+b-y)^{2}$

위 식을 통해 얻은 값을 최소화 시키는 방향으로 $w, b$를 조정한다.

경사하강법

위의 MSE의 식을 전개하여 풀기이는 데이터 크기가 커질수록 복잡도가 크게 증가하여 비효율적이다.

따라서 경사하강법^{gradient descent} 을 사용하여 $w$를 구한다.

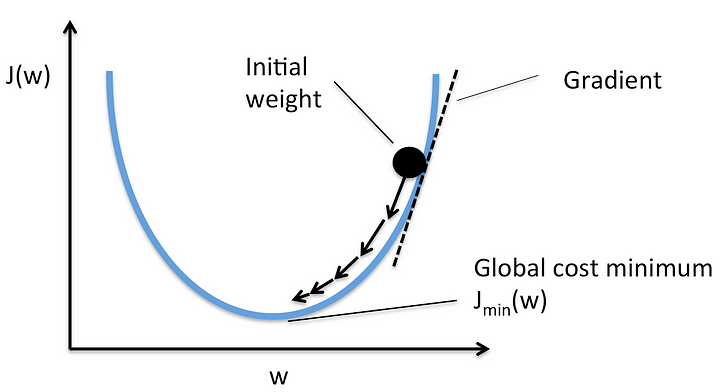경사하강법^[1]

방정식의 미분을 통해 순간 기울기를 얻을 수 있다.

지속적인 기울기, $w$ 업데이트를 통해 오차의 극소값 찾을 수 있다.

$w_{t+1} = w_{t} - gradient \times learning rate$

여기서 학습률^{learning rate} 이란 변수 $w$를 얼만큼 업데이트할지 결정하는 수치이다.

학습이 진행됨에 따라 최종적으로 오차를 최소화하는 $w$로 수렴하게 된다.

pytorch로 경사하강법 구현

https://github.com/maizer2/First-step-on-the-Pytorch/blob/master/Chapter3_Linear_Regression/%EC%84%A0%ED%98%95%ED%9A%8C%EA%B7%80%EB%B6%84%EC%84%9D.ipynb

참고문헌

1. 경사 하강법에서 마이너스, ICHI.PRO, 2022.04.05 방문, https://ichi.pro/ko/gyeongsa-hagang-beob-eseo-maineoseu-54562797399893

← 이전 글로 다음 글로 →