Why convert to a Non-Linear Function?

인공신경망을 훈련하기 위해서는 Weight와 Bias를 수정하는 과정이 필요하다.

Weight와 Bias를 통해 계산된 값은 단순한 1차 함수로 선형 값을 가지게된다.

선형 함수를 사용하면 최소값을 알 수 없는데 이를 해결하기 위해 비선형 함수로 변환해주는 과정이 발생한다.

왜 비선형 함수를 사용하면 최소값을 알 수 있을까?

\[f(x) = wx + b\]

단순한 비선형 그래프인 2차함수^[1]를 예로 들자면 그림과 같이 최소값을 가지는 지점이 발생한다.

2차 함수는 한개의 미지수 값을 입력으로 받는 함수를 의미하고 2차원 데이터로 표현된다.

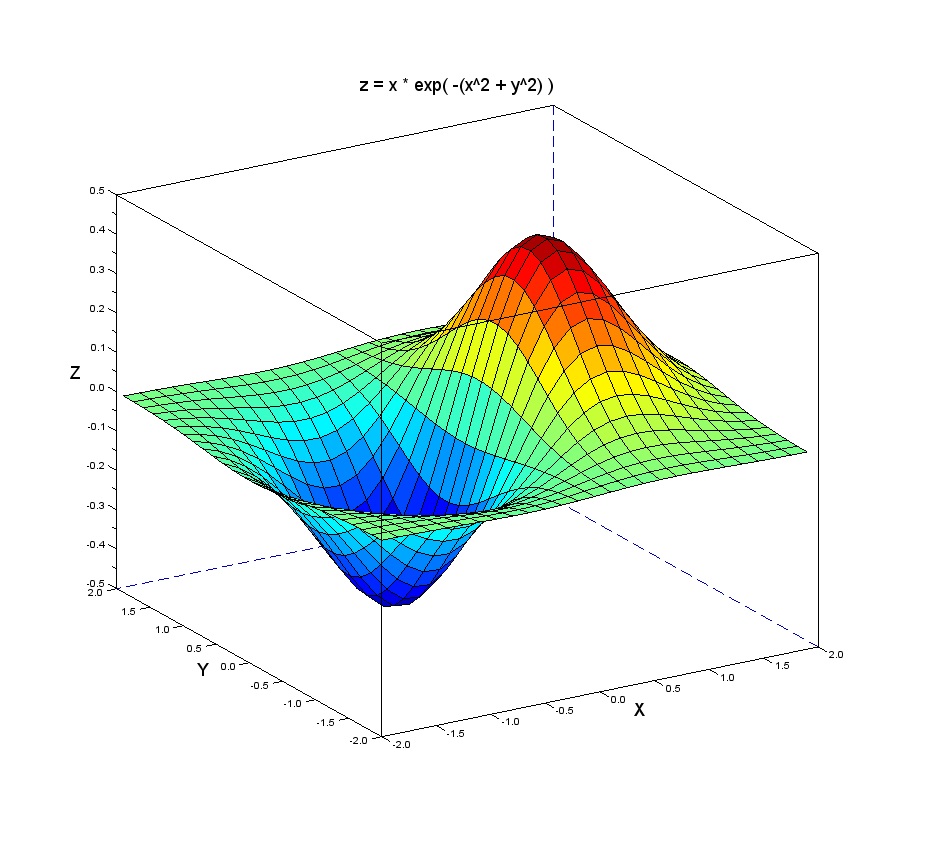
3D Fucntion

\[f(x, y) = ax + by + c\]

만약 두개의 미지수를 입력으로 받는 함수라면 다음과 같이 3차원^[2] 데이터로 표현이 될 것이다.

신경망에서 지수값이 많아짐에 따라 차원이증가해서3차원, 4차원 시각적으로 표현하지못하고 사람이 인식하지 못하는 수준에 가더라도 비선형 그래프는 최소값을 가지는 지점이 존재하게된다.

이 Non-Linear Graph의 최소값을 찾아가기 위해 고안된 Algorithm이 바로 Gradient Descent Algorithm이다.

신경망은 단순히 Linear Function이므로 최소값을 찾을 수 없다.

Linear Function을 Non-Linear Function에 합성하면 다음과 같게된다.

\[f(g(w))\]

Linear Function인 $g(w)$가 Non-Linear Function $f(y)$를 통과하며 Non-Linear Function으로 변환된다.

Non-Linear Function의 최소값을 찾는 과정인 Gradient Descent Algorithm을 사용하면 Function의 최소지점으로 도달할 수 있게된다.