들어가기 전에

나한테 가설함수나 비용함수는 정말 미칠것 같은 갈증의 대상이였다.

인공지능을 공부하면서 가설함수 비용함수를 왜 쓰는지는 알겠지만 표면적으로만 알고 내부적인 내용을 이해할 수 없었다.

아무리 찾아봐도 대충 설명하고 넘어가는게 너무 많아 혼란만 불러일이킬 뿐이였다.

하지만 우연히 쿠버네티스 공부를 위해 쿠브플로우 쿠버네티스에서 머신러닝이 처음이라면! 책을 읽게 되었는데, 가설함수를 이해하기 쉽게 써놓으셨다.

이책을 먼저 봤다면 …

서론

가설함수, Hypothsis Function $ H(x) $은 주어진 데이터를 $X$와 $Y$ 사이의 관계를 통해 실제 값과의 관계를 찾아내는 것이다.

$f(x)$는 실제 값이고 $H(x)$는 가설 값이다.

\[y = f(x)\] \[\hat{y} = H(x)\]

이 함수 표현에 속지말자, 이 함수를 모든 데이터에 적용하려다 보니 난 정말 먼길을 돌아왔다.

데이터들의 집합들을 함수로 표현하는 과정을 통해 가설함수를 만들 수 있다.

실제 값이 아닌 가설 함수를 통해 가격 값 측정하기

한가지 값에 한개의 값만

과일 가격
사과 1,200

위 표를 함수로 표현하면 아래와 같다.

\[H(사과) = 1,200\]

만약 과일과 가격이 미지수라면? $ y = f(x) $로 표현할 수 있다.

하지만 n가지 값에 n개의 값은?

과일 가격
과일 세트1 1,200, 1,000, 500, 600

이렇게 x값이 여러개일 경우는?

\[x = (사과, 배, 딸기, 귤)\] \[H(x) = (1,200 + 1,000 + 500 + 600)\]

다음과 같이 벡터로 표현이 가능하고 다음과 같이 벡터의 내적으로 표현할 수 있다.

\[H(x) = \begin{bmatrix} 1,200 + 1,000 + 500 + 600\\ \end{bmatrix} = [1개 1개 1개 1개] \cdot \begin{bmatrix} 사과\\ 배\\ 딸기\\ 귤\\ \end{bmatrix}\]

다음과 같이 표현할 수 있지만 가설함수는 다음과 같이 표현한다.

한가지 값을 가설 함수로 표현

여기서 W는 Weight(가중치), b는 bias(편항)

과일 가격
사과 $H(사과)$
\[H(사과) = W \cdot 사과 + b\]

어떻게 해석할 수 있을까?

가중치와 편향이 없는 사과 가격은 원가 1,200원 일 것 이다.

하지만 어떤 외부 요인에 의해 가중치와 편향이 추가 됐다면 시장 가격값이 변할 것이다.

n가지 과일을 가설 함수로 표현

과일 가격
과일 세트1 1,200, 1,000, 500, 600

행렬은 이런 값의 모음(집합)을 수학적으로 잘 표현 할 수 있다.

\[x = (사과, 배, 딸기, 귤)\] \[H(x) = [W_{사과} W_{배} W_{딸기} W_{귤}] \cdot \begin{bmatrix} 사과\\ 배\\ 딸기\\ 귤\\ \end{bmatrix} + b\] \[H(사과, 배 딸기, 귤) = (W_{사과} \cdot 사과) + (W_{배} \cdot 배) + (W_{딸기} \cdot 딸기) + (W_{귤} \cdot 귤) + b\]

목적에 맞는 가설 함수를 사용한 비용 함수의 그래프

주의!!! 어떤 가설 함수, 비용 함수를 선택하는지에 따라 그래프의 모양과 함수의 모양이 변한다

어떤 비용 함수를 사용하는지에 따라 그래프는 변한다.

가장 기초적인 Linear Regression, Logistic Regression 부터 Ridge, Lasso, polynomial … 다양하다

기초적인 선형과 로지스틱의 가설함수를 식과 그래프로 본다.

** 가설함수만 표현했을 뿐 비용 함수는 표현하지 않았다. **

\[Linear(x) = Wx + b\]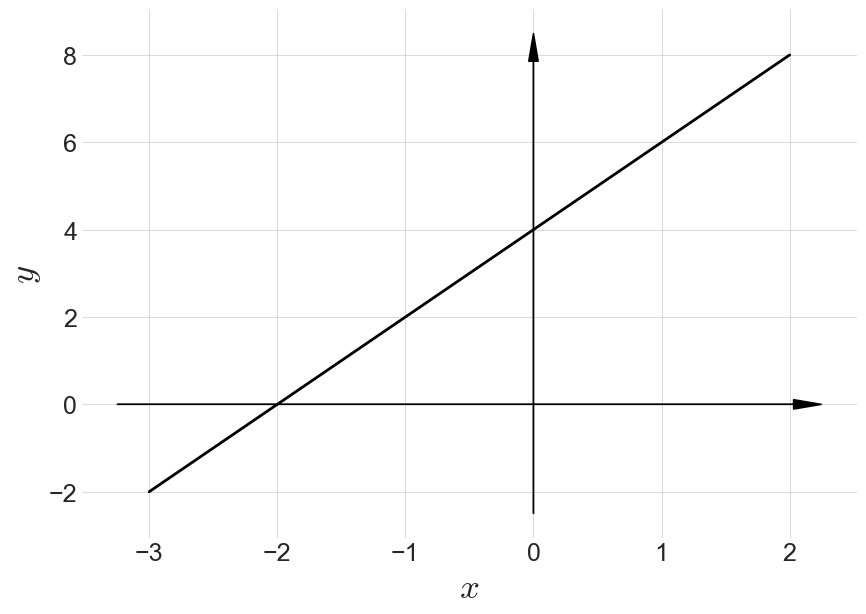

1차함수

Linear Regression Function[1]


\[Logistic(x) = \frac{1}{1+e^{-W^{T}x}}\]

Logistic Fucntion

Logistic Regression Function[2]


참고 문헌

1. 파이썬으로 1차함수 그래프 그리기, 캐리의 데이터 세상, 2021.04.25 작성, 2022.05.04 방문, https://carriedata.tistory.com/entry/파이썬으로-1차함수-그래프-그리기

2. Logistic Regression,Jaejoon’s Blog, 2019.01.09 작성, 2022.05.04 방문, https://lee-jaejoon.github.io/stat-logistic/